Joint Architecture Standard Overview Profile
Entangled Networks
Entangled networks are a class of networks that attempt to maximize the algebraic connectivity of the topology. These networks can be constructed with explicit complex mathematical methods or approximated by a repetitive random optimization algorithm (which is the method chosen for this analysis) (see Figure).
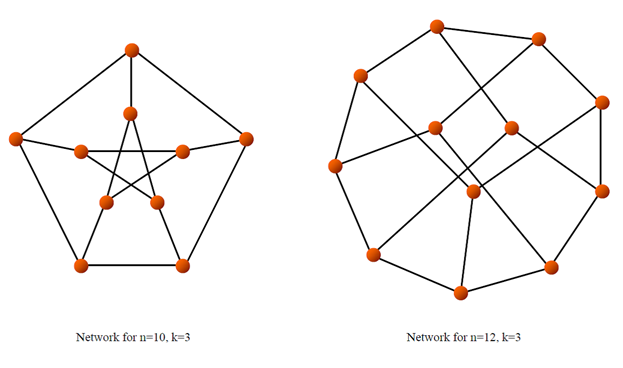
Sample Entangled Networks
The repetitive random optimization algorithm takes a topology and randomly rewires two links. The algebraic connectivity of the new rewired graph is calculated. If the new graph has a larger algebraic connectivity the rewiring is made permanent. However, if the rewiring does not result in a higher algebraic connectivity value, the original graph is restored. This rewiring is repeated many times until the topology shows no further improvement to rewiring.
These graphs are considered to be optimal with respect to algebraic connectivity. Since algebraic connectivity is related to average path length and diameter as well as failure rate and reliability, maximizing this value for a given node degree should yield the most (or one of the most) reliable, best performing topology given the available resources.
- Advantages: Theoretically these topologies are optimal in balancing average path length and connectivity for given node count and node degree. The number of nodes as well as the degree of nodes is completely variable and may be set to any value prior to the optimization process.
- Disadvantages: Robust routing algorithm is required. Due to the random nature of the optimization process, as well as the possibility of encountering local minima/maxima in this process, a truly optimal network cannot be guaranteed unless one is explicitly constructed (note, too, explicit construction introduces a fair number of other constraints). For larger networks, optimization may take some time.
