Joint Architecture Standard Overview Profile
Complete and Incomplete Hypercubes
An overall good performer, hypercubes are very reliable and offer good performance. Complete hypercubes have fixed size of 2^d (i.e., 4, 8, 16, 32, 64, etc, nodes) but an extension to this structure (incomplete hypercubes) allows for arbitrary size.
Hypercubes are constructed by beginning with two interconnected nodes (a 1-D hypercube) (see Figure). If more nodes are required, the structure is duplicated and interconnected by adding links between the original and the duplicated nodes.
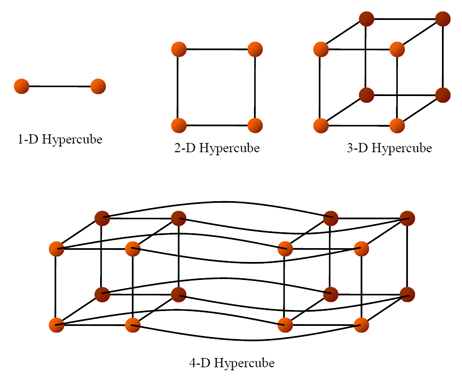
Complete Hypercubes (d=1,2,3, and 4)
Node degree grows quickly, making node complexity an issue for larger networks. Link count also exceeds other topologies for similar node counts.
Hypercubes offer excellent connectivity, especially at large node counts. This topology also has a high probability of withstanding random link/node failures.
Incomplete hypercubes relax the requirements of complete hypercubes to allow for structures that resemble hypercubes without the strict node count constraint. They generally perform about as well as complete hypercubes.
Reliability in incomplete hypercubes, however, is somewhat unpredictable. Incomplete hypercubes slightly larger than 2^d will introduce points of failure and decrease reliability, while hypercubes slightly smaller than 2^d will perform almost as reliably as a complete hypercube of size 2^d.
As an example, look at the figure below for an incomplete hypercube of N=9; if the link between nodes 1 and 9 were to fail, or if node 1 were to itself fail, then node 9 would be isolated from the rest of the network. Thus, the failure of one node causes two nodes to “fail” (or, the failure of a single link would additionally cause one node to “fail”). However, for networks closer in size to 2^d (such as the above case where N=7), the reliability of the hypercube is closer to that of a hypercube with d=3 (N=8).
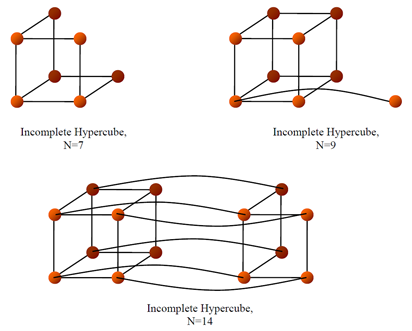
Incomplete Hypercubes (n=7, 9, and 14)
The problem of variable reliability could be solved somewhat by adding links to the “incomplete” portion of the topology. However, this is an “impure” solution and adding these additional links makes the resulting topology deviate from the hypercube model.
- Advantages: Complete hypercubes offer good to very good performance, very good fault tolerance, and easy algorithms exist for routing traffic through hypercubes. Incomplete hypercubes have performance at near-complete-hypercube level and can have an arbitrary number of nodes. Easy routing algorithms also exist for incomplete hypercubes.
- Disadvantages: Node degree grows quickly as the number of nodes increase. Incomplete hypercubes have unpredictable reliability. Link counts grow faster than other topologies, perhaps indicating that a more optimal topology could be used at higher node/link counts.
